Código
library(Rspotify)
library(dplyr)
library(ggplot2)
library(rstanarm)Bruno Santos
8 de junho de 2020
Diante do atual cenário de isolamento durante a quarentena devido à pandemia da Covid-19, é interessante pensarmos em maneiras de contornar alguns dos desprazeres de estarmos longe fisicamente dos nossos amigos e familiares. Para mim uma das soluções para resolver esse probleminha é ouvir uma boa música. Embora a definição de “boa música” possa variar de pessoa pra pessoa, nesse post vamos utilizar uma informação objetiva sobre músicas “felizes”, conforme uma variável que é fornecida pela API do Spotify.
Segundo o manual de referência de uso da API do Spotify, existe uma variável atribuída a cada música no aplicativo, chamada valence, que tem sua definição traduzida livremente aqui:
Uma medida de 0.0 a 1.0 descrevendo a positividade musical transmitida por uma música. Músicas com alto valor de valência soam mais positivas, enquanto que músicas com baixo valor de valência soam mais negativas.
Considerando então essa informação de valência de uma amostra de músicas, vamos construir um modelo estatístico para tentar identificar características (ou covariáveis) que ajudem a explicar essa positividade (variável resposta) nas músicas para então construir uma nova playlist.
Vamos considerar os seguintes pacotes para essa análise.
O pacote Rspotify é utilizado para buscar as músicas na API do Spotify. O pacote dplyr é necessário para todas as operações de selecionar, renomear, filtrar, entre outras, que são feitas no banco de dados ao longo da análise. O pacote ggplot2 nos ajuda a fazer os gráficos de maneira prática e fácil. E o pacote rstanarm é utilizado para estimar os modelos bayesianos que serão empregados para construir uma nova playlist.
Para ter acesso às músicas, é preciso obter uma chave de acesso conforme descrição nesse link. Após obtenção dessa chave, essa informação deve ser colocada no objeto keys utilizando a função Rspotify::spotifyOAuth().
Embora a API do Spotify não explique exatamente como funciona o algoritmo para definir a valência de cada música, entendemos que tal algoritmo deva utilizar de alguma maneiras as letras das músicas consideradas. Sendo assim e supondo que esse treinamento talvez esteja mais calibrado para músicas em inglês, vamos nos limitar a músicas de língua inglesa, inicialmente. A quem tiver interesse, fica aqui a sugestão de reprodução desse exercício para músicas brasileiras, por exemplo.
Para estimarmos nosso modelo vamos considerar somente uma amostra de músicas. Com o intuito de utilizarmos músicas mais recentes e que tenham maior alcance, utilizaremos as 100 músicas da lista da “Billboard Hot 100”, que é um importante referencial no mundo da música. Nossos dados consideram as musicas dessa lista obtidas no dia 05/06/2020.
Em seguida, obtemos as variáveis referentes a cada uma das músicas:
Para facilitar a leitura e discussão dos resultados, vamos renomear as variáveis
Em seguida, vejamos a distribuição de valores da nossa variável resposta a partir do seu histograma, assim como uma estimativa da densidade dessa distribuição.
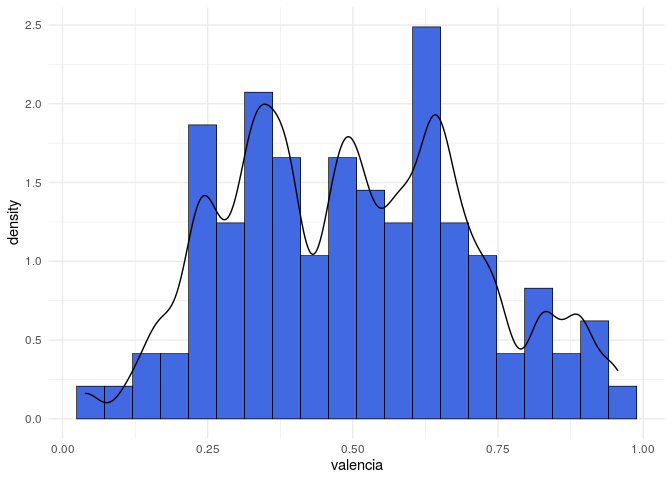
Tendo em vista a dificuldade de se modelar a variabilidade dessa variável resposta, embora existam opções como a regressão beta, i.e., quando assumimos que a variável resposta tem distribuição beta, vamos considerar uma simplificação do problema. Em vez de modelar essa variável em sua escala contínua, iremos considerar uma categorização dessa variável, em que criamos uma variável dicotômica, em que separamos as observações entre aquelas com valor maior ou menor que 0,5, valor que está bastante próximo da mediana dos dados.
Tendo uma variável dicotômica, podemos pensar em estimar um modelo para uma variável resposta com distribuição Bernoulli. Aproveitando a discussão aqui da Prof. Agatha, em um post anterior a esse, temos o interesse em construir um modelo preditivo - supondo a construção de uma playlist ao fim dessa análise, porém vamos nos ater a um modelo explicável. Essa escolha é simplesmente por simplificação do problema, embora em uma oportunidade futura podemos rever essa escolha. Temos então para a variável resposta \(Y = 1\), se a música é mais positiva (valência > 0,5), e \(Y = 0\), caso contrário.
Supomos que \(P(Y = 1) = p\) e utilizando o modelo de regressão logístico podemos escrever essa probabilidade como
\[\begin{equation} p = \frac{e^{X\beta}}{1 + e^{X\beta}}, \end{equation}\]
em que colocamos na matriz de planejamento X nossas covariáveis. Nosso interesse é estimar o vetor \(\beta\) segundo a nossa amostra de 100 músicas. Uma vez com beta estimado e a depender dos valores de X de uma dada música, podemos então estimar a probabilidade da música ser positiva ao considerar a relação dada na equação acima.
Antes de estimar o modelo, podemos checar se as covariáveis (após uma padronização dos seus valores) possuem algum tipo de correlação alta entre si, fazendo por exemplo:
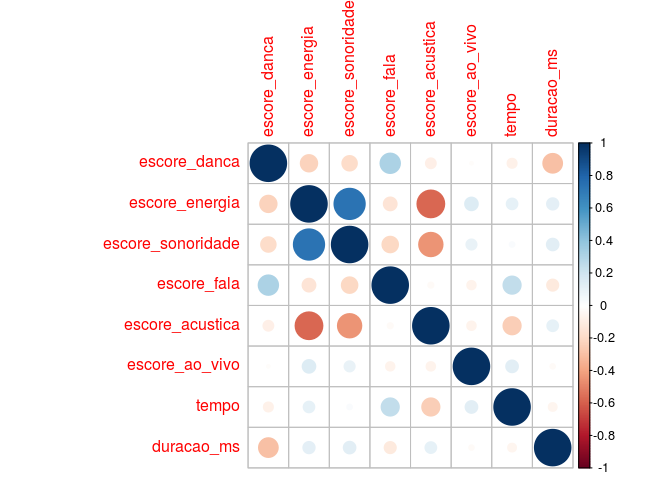
A análise do gráfico anterior nos mostra que as variáveis escore_sonoridade e escore_energia têm uma correlação alta. Apesar disso, vamos manter as duas variáveis na matriz de planejamento \(X\), porém nos atentaremos às estimativas do modelo.
Para estimação dos parâmetros do modelo vamos considerar a inferência bayesiana, através do pacote rstanarm. Uma introdução básica ao tema pode ser vista no link. Para a definição das nossas crenças a priori sobre o vetor de parâmetros \(\beta\), consideramos uma distribuição t-Student com 7 graus de liberdade, conforme discussão feita aqui.
data_model <- variaveis_preditoras
data_model$outcome <- todas_musicas$valencia_cat
## Estimando modelo logístico bayesiano
t_prior <- student_t(df = 7)
modelo <- stan_glm(outcome ~ .,
data = data_model,
family = binomial(link = "logit"),
prior = t_prior, prior_intercept = t_prior,
QR = FALSE,
seed = 12345678, refresh = 0
)Podemos verificar densidades das distribuições a posteriori dos parâmetros, fazendo
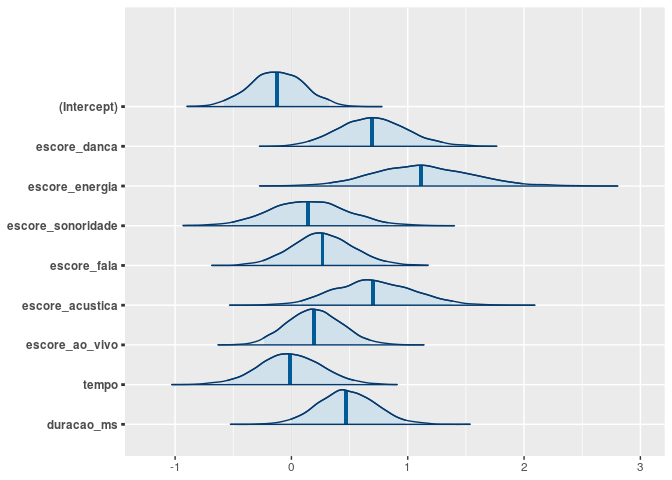
E se quisermos as estimativas pontuais e também os respectivos intervalos de credibilidade, podemos utilizar o seguinte:
| Coefficient | |
|---|---|
| (Intercept) | -0.12345838 |
| escore_danca | 0.69537783 |
| escore_energia | 1.11227711 |
| escore_sonoridade | 0.14325884 |
| escore_fala | 0.26609762 |
| escore_acustica | 0.69828862 |
| escore_ao_vivo | 0.19340754 |
| tempo | -0.01454859 |
| duracao_ms | 0.47230439 |
| 2.5% | 97.5% | |
|---|---|---|
| (Intercept) | -0.582274955 | 0.3213192 |
| escore_danca | 0.146963038 | 1.2945369 |
| escore_energia | 0.326135738 | 1.9850818 |
| escore_sonoridade | -0.510518128 | 0.8271121 |
| escore_fala | -0.244289928 | 0.8136716 |
| escore_acustica | 0.080733371 | 1.3837728 |
| escore_ao_vivo | -0.238027585 | 0.6713185 |
| tempo | -0.550411657 | 0.5339127 |
| duracao_ms | -0.002269076 | 0.9785030 |
Tendo em vista os intervalos de 95% de credibilidade, diríamos que os parâmetros associados às covariáveis escore_danca, escore_energia e escore_acustica contribuem positivamente para a razão de chances entre músicas mais positivas e menos positivas, conforme aumentamos os valores dessas variáveis. Esse é um aspecto do modelo logístico, em que podemos interpretar os valores dos parâmetros obtidos. Nesse caso, diríamos que quanto maior os valores dessas variáveis maior a chance de observamos uma música positiva.
Supondo que a variável resposta seja em parte explicada pelas letras da música, mas em outra parte possa ser entendida como funcões das variáveis explicativas que escolhemos como, por exemplo, escore_danca e escore_energia, podemos fazer a previsão dessa probabilidade de observarmos uma música mais positiva considerando uma amostra de músicas brasileiras. Para fazer esse exercício, consideramos uma playlist com músicas brasileiras dos últimos anos, que segundo a definição do Spotify tem
Hits brasileiros dos últimos anos para animar sua faxina.
Sendo assim, gostaríamos de selecionar aquelas com maiores valores a probabilidade de ser positiva baseado nos coeficientes do objeto modelo que estimamos anteriormente. Poderíamos eventualmente selecionar dentre todos os modelos que foram estimados, aquele com a maior discrimação, porém vamos deixar esse tipo de análise para posts futuros. Podemos obter as músicas e suas respectivas variáveis da mesma maneira que fizemos anteriormente.
musicas_dia_faxina <-
Rspotify::getPlaylistSongs(
user_id = "Billboard",
playlist_id = "37i9dQZF1DXdg3JLYhYrif",
token = keys
)
variaveis_musicas_faxina <-
lapply(musicas_dia_faxina$id, getFeatures, token = keys)
todas_musicas_faxina <- do.call(rbind.data.frame, variaveis_musicas_faxina) %>%
select(-uri, -analysis_url)
variaveis_predicao <- todas_musicas_faxina %>%
rename(
escore_danca = danceability,
escore_energia = energy,
escore_sonoridade = loudness,
escore_fala = speechiness,
escore_acustica = acousticness,
escore_ao_vivo = liveness,
tempo = tempo,
duracao_ms = duration_ms,
valencia = valence
) %>%
select(
escore_danca, escore_energia, escore_sonoridade, escore_fala, escore_acustica,
escore_ao_vivo, tempo, duracao_ms
) %>%
scale()Aqui estamos supondo que as escalas das variáveis do banco de dados que foi utilizado para estimação do modelo e desse banco de dados que usaremos para as previsões são similares, mas isso poderia ser investigado com mais cuidado. Além disso, esse exercício de previsão poderia ser considerado dispensável, dado que temos disponível a variável valencia também para as variáveis dessa playlist. Porém, supondo que os coeficientes estimados no modelo anterior conseguem explicar parte da variabilidade da positividade das músicas em geral, entendemos que esse modelo possa ser utilizado no caso brasileiro.
Dessa forma, podemos obter as previsões das probabilidades fazendo o cálculo das probabilidades:
X <- as.matrix(cbind(1, variaveis_predicao))
preditor_linear <- X %*% matrix(coef(modelo), ncol = 1)
numerador <- exp(preditor_linear)
denominador <- 1 + numerador
top_10 <- musicas_dia_faxina %>%
mutate(probabilidades = as.numeric(numerador / denominador)) %>%
arrange(desc(probabilidades)) %>%
select(artist_full, tracks, probabilidades) %>%
slice(1:10)
knitr::kable(top_10)| artist_full | tracks | probabilidades |
|---|---|---|
| Seu Jorge | Amiga Da Minha Mulher | 0.9745518 |
| Henrique & Diego feat. Dennis DJ | Malbec (Part. Dennis Dj) (feat. Dennis DJ) - Ao Vivo | 0.9198087 |
| Zé Felipe feat. Menor | Você Não Vale Nada | 0.8787458 |
| João Lucas & Marcelo feat. MC K9 | Louquinha (feat. MC K9) | 0.8498655 |
| MC Guime feat. Emicida | País do Futebol | 0.8496449 |
| Thiaguinho feat. Ludmilla | Só Vem! - Ao Vivo | 0.8473463 |
| Atitude 67 | Cerveja De Garrafa (Fumaça Que Eu Faço) - Ao Vivo | 0.8346313 |
| Maiara & Maraisa | 10% - Ao Vivo | 0.8227158 |
| POCAH | Não sou obrigada | 0.8210113 |
| MC Loma e As Gêmeas Lacração | Envolvimento | 0.8205628 |
Essas seriam então as dez músicas com maiores probabilidades segundo o modelo construído anteriormente. Poderíamos fazer algumas perguntas pra esses resultado: * estaria o modelo fazendo sentido de alguma maneira? * Seria razoável utilizar os coeficientes estimados nessa outra base de dados? * Poderíamos ter considerado critérios de seleção de variáveis e de regularização dos coeficientes. Qual o efeito dessas escolhas nesse problema?
Todas essas questões são pertinentes e poderão ser tratadas em posts específicos no futuro. Nesse momento, gostaríamos apenas de ressaltar a possibilidade de utilizarmos modelos probabilísticos para fazer uma tarefa que talvez não usual, como pensar numa playlist no Spotify. Aqui também aproveitamos para mostrar também como fazer esse tipo de consultas usando a respectiva API.
Com relação à escolha do valor intermediário em que fixamos o valor igual a 0,5, podemos variar essa quantidade e verificar se nossa inferência com relação aos parâmetros se altera. Para isso, podemos utilizar os quantis da variável valencia conforme:
Podemos usar o objeto quantis_valencia e estimar o modelo diversas vezes, guardando as estimativas obtidas ao final, assim como o valor da variável resposta utilizada.
resultados <- lapply(1:length(quantis_valencia), function(a) {
todas_musicas <- todas_musicas %>%
mutate(valencia_cat = cut(valencia, c(0, quantis_valencia[a], 1)))
data_model$outcome <- todas_musicas$valencia_cat
modelo_lista <- stan_glm(outcome ~ .,
data = data_model,
family = binomial(link = "logit"),
prior = t_prior, prior_intercept = t_prior,
QR = FALSE,
seed = 12345678, refresh = 0
)
coeficientes <- coef(modelo_lista)
intervalos <- posterior_interval(modelo_lista, prob = 0.95)
valores <- tibble(
coef = coeficientes,
lim_inf = intervalos[, 1],
lim_sup = intervalos[, 2],
valor_quantil = sequencia_quantis[a]
)
valores <- mutate(valores, nome = names(coeficientes))
valores
})
todas_estimativas <- do.call(rbind.data.frame, resultados)
g <- ggplot(todas_estimativas, aes(x = valor_quantil)) +
theme_minimal()
g + geom_line(aes(y = coef)) +
geom_line(aes(y = lim_inf), linetype = 2) +
geom_line(aes(y = lim_sup), linetype = 2) +
facet_wrap(~nome) +
xlab("Quantis de valencia") + ylab("Coeficientes e intervalo de credibilidade de 95%")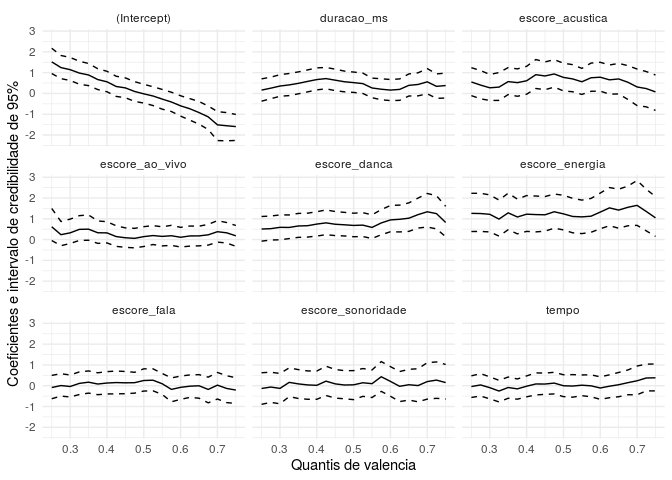
O resultado mostrado no gráfico acima é interessante pois mostra que independente da escolha que fizéssemos pra o ponto de corte, quando criamos a variável categórica, teríamos obtido as mesmas estimativas praticamente, com exceção de alguns valores mais extremos dos quantis. Com relação ao intercepto, é natural a variação observada tendo em vista a interpretação desse parâmetro para o modelo logístico.