Usando animações para entender conceitos estatísticos: o passeio aleatório do Pacman
Para diversos conceitos estatísticos, em muitos casos é importante fazer um gráfico para ilustrar a ideia que gostaríamos de passar. Para distribuições de probabilidade com mesma média e variâncias diferentes, é interessante mostrar uma comparação entre as funções de probabilidade ou densidade em cada um dos casos. Outro exemplo é quando estamos falando de regressão e queremos apresentar as diferentes distribuições condicionais de probabilidade. Inclusive considerando a hipótese de que mais aulas online serão necessárias nos próximos meses, é importante pensar em maneiras diferentes de apresentar certos resultados.
Hoje vamos mostrar o pacote gganimate, em
que é possível é possível construir gifs ou vídeos ilustrando alguns
desses conceitos.
Primeiramente, carregando o pacote de interesse e outros que vamos utilizar:
library(gganimate)
library(dplyr)
library(ggimage)
O pacote ggimage
é utilizado para adicionarmos imagens aos gráficos do pacote
ggplot2.
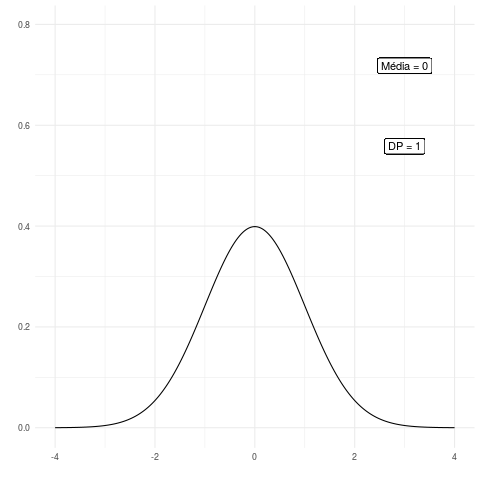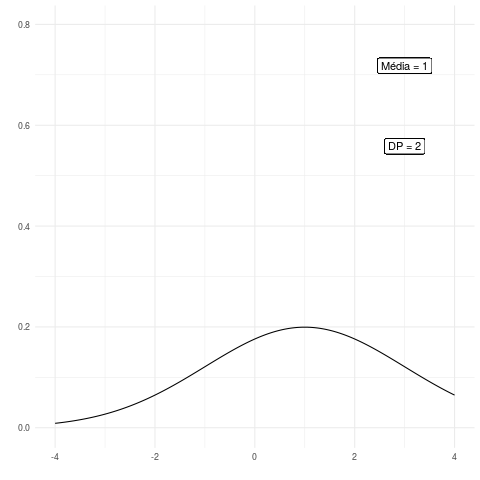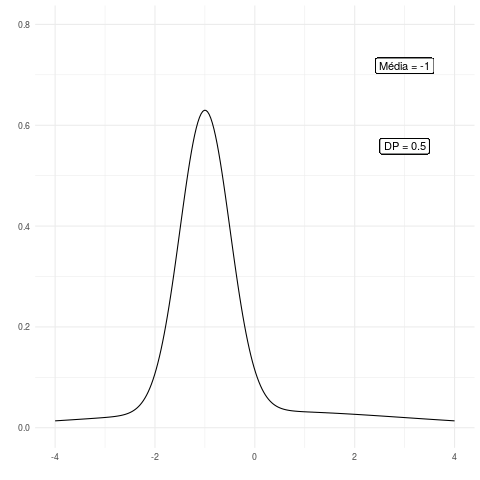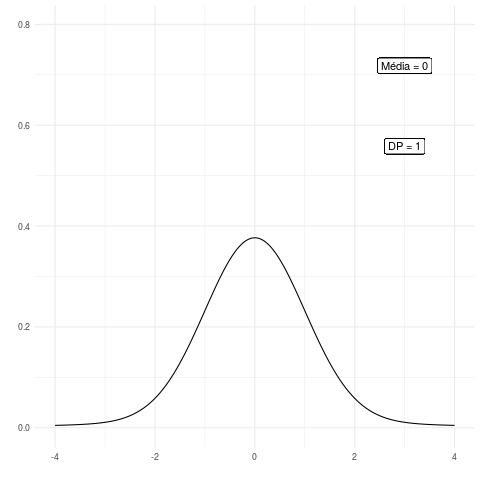
Agora vamos fazer uma animação para mostrar a diferença da distribuição normal conforme mudamos os seus parâmetros. Veja o código a seguir em que geramos os valores para as diferentes distribuições de probabilidades:
medias <- c(0, 1, -1, 0)
desvios_padrao <- c(1, 2, 0.5, 3)
numero_casos <- length(medias)
grid_x <- seq(-4, 4, length.out = 250)
valores_normais <- lapply(1:numero_casos, function(a){
y <- dnorm(grid_x, mean = medias[a], sd = desvios_padrao[a])
data.frame(x = grid_x, y = y, caso = a,
media = paste0("Média = ", rep(medias[a], length(grid_x))),
sd = paste0("DP = ", rep(desvios_padrao[a], length(grid_x))))
}) %>% do.call(rbind.data.frame, .)
valores_normais <- valores_normais %>%
mutate(pos_x = 0.75 * max(x),
pos_y1 = 0.9 * max(y),
pos_y2 = 0.7 * max(y))
Em seguida criamos um gráfico utilizando o ggplot2 de maneira usual.
Colocamos também labels para identificar qual média e desvio padrão
está sendo utilizado para gerar o respectivo gráfico
g <- ggplot(valores_normais, aes(x = x, y = y)) +
scale_colour_viridis_c() +
geom_label(aes(x = pos_x, y = pos_y1, label = media)) +
geom_label(aes(x = pos_x, y = pos_y2, label = sd)) +
geom_line() + theme_minimal() +
ylab("") + xlab("")
E por último utilizamos a função transition_states do pacote
gganimate para dar a animação aos gráficos.
animacao <- g +
transition_states(caso,
transition_length = 1,
state_length = 1)
Podemos utilizar em seguida a função gifski_renderer() para gerar um
gif. O resultado pode ser visto a seguir:
animacao_normal <- animate(animacao, renderer = gifski_renderer(),
width = 480, height = 480)
animacao_normal
Se temos interesse em salvar o gif para usar posteriormente, podemos
utilizar a função anim_save().
anim_save("animacao_normal.gif", animacao_normal)
Note que uma das curvas passa a impressão de ter um comportamento assimétrico, porém isso é simplesmente devido ao fato de fixarmos os valores na escala x entre -4 e 4. Desse modo, as escalas ficam sempre fixas e não podemos perceber visualmente a propriedade de simetria dessa distribuição.
É possível contornar essa especificidade da escala fixa usando a função
view_follow(). Para ilustramos essa função, consideremos uma situação
inusitada em que gostaríamos de observar uma “corrida” entre duas
distribuições normais com mesma média. Nesse caso somente a média das
duas distribuições se altera, porém podemos fazer com essas médias
aumentam com taxas diferentes. Isso dá a impressão inesperada de uma
distribuição “ultrapassar” a outra. Veja o código a seguir:
quantis <- 1:299/300
numero_medias <- 15
medias1 <- seq(20, 30, length.out = numero_medias)
medias2 <- seq(15, 35, length.out = numero_medias)
normais_media <- lapply(1:numero_medias, function(a){
x1 <- qnorm(quantis, mean = medias1[a])
x2 <- qnorm(quantis, mean = medias2[a])
y1 <- dnorm(x1, mean = medias1[a])
y2 <- dnorm(x2, mean = medias2[a])
data.frame(x = c(x1, x2), y = c(y1, y2), group = a,
tipo = rep(c(1, 2), each = length(quantis)))
}) %>% do.call(rbind.data.frame, .)
g <- ggplot(normais_media, aes(x = x, y = y, group = tipo, colour = tipo)) +
scale_colour_viridis_c() +
geom_line(size = 1.25) + theme_minimal() +
theme(legend.position = 'none',
axis.text.y = element_blank()) +
ylab("") + xlab("")
corrida <- g +
transition_states(group,
transition_length = 0.5,
state_length = 0) +
view_follow() +
ease_aes("linear")
corrida_normais <- animate(corrida, renderer = gifski_renderer(),
width = 480, height = 480)
corrida_normais
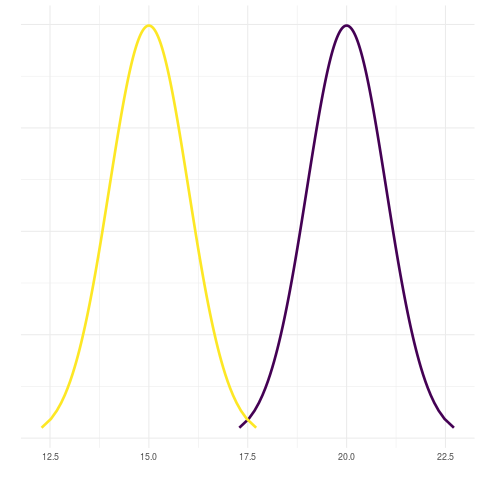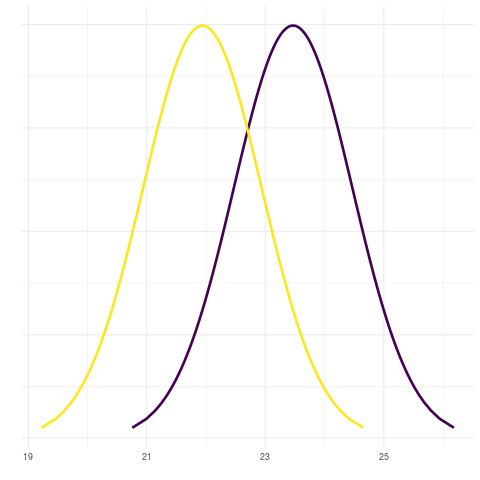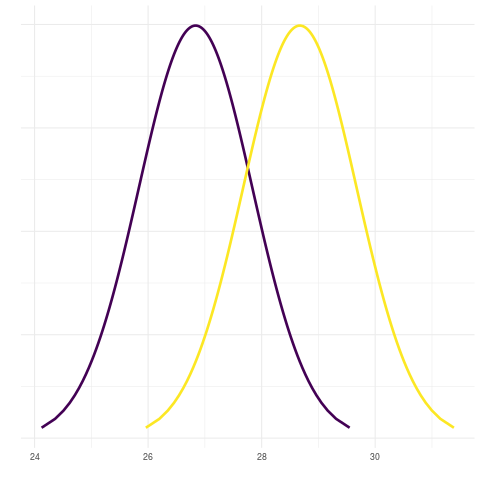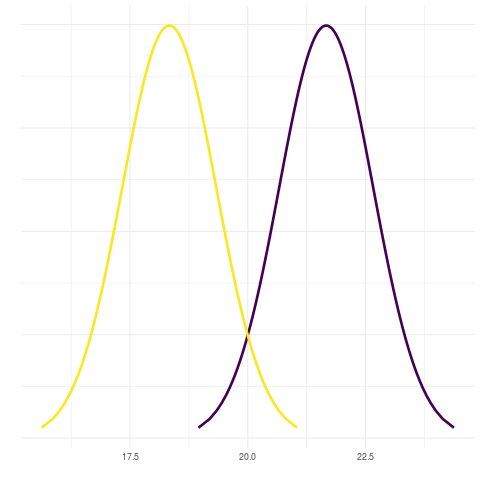
Note como após algum tempo a curva que inicia com menor valor médio termina a animação com maior valor médio, dando a impressão de ter então “ultrapassado” a outra curva.
Um outro conceito importante que pode ser exemplificado a partir de animações, facilitando a sua compreensão se refere à ideia de distribuições condicionais de probabilidade na análise de regressão. Por exemplo, considere uma variável resposta como tempo de incubação de um certo vírus. Suponha a relação entre essa variável resposta e idade de uma pessoa for crescente segundo algum coeficiente, ou seja, conforme aumenta-se o valor de idade, aumenta-se em média o valor do tempo de incubação. Suponha também que a incerteza sobre a variável tempo de incubação possa ser descrita por uma distribuição normal, logo a seguinte ilustração poderia ser feita.
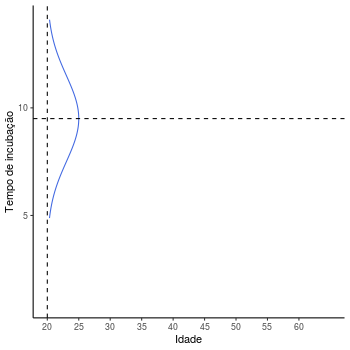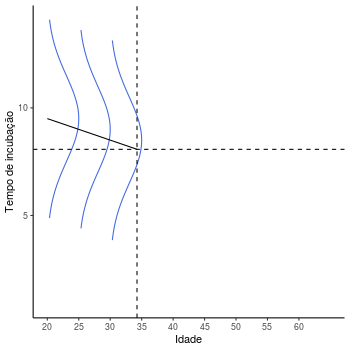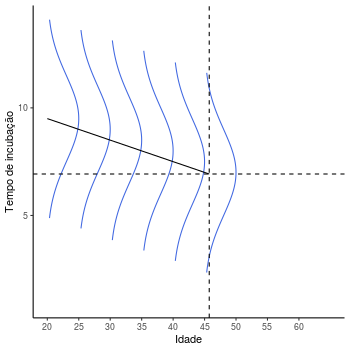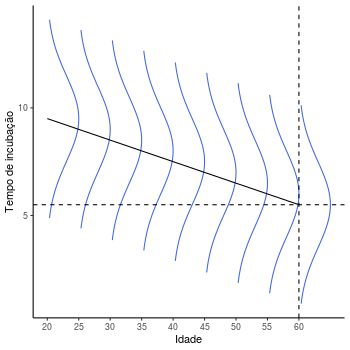
A reta representada é construída através das médias condicionais de cada
uma das distribuições, conforme suposição no modelo de regressão linear.
Essa animação também pode ser feita com o pacote gganimate, porém
deixaremos o código como exercício para as pessoas interessadas.
Por último, podemos ilustrar um fenômeno importante na estatística que pode ser definido como passeio aleatório. De forma bem simplificada, poderíamos definir que um partícula move para a esquerda com mesma probabilidade. Ao chegar no seu destino, esta faz de novo a decisão de mover-se para esquerda ou direita com as mesmas probabilidades. Suponha que essa partícula seja o personagem Pacman dos videogames (imagem “pacman.png” obtida em https://www.gratispng.com/png-1k10z2/). Nesse caso, poderíamos fazer a seguinte animação para ilustrar uma possível trajetória do personagem com 30 passos.
tamanho_passeio <- 30
passos <- c(-1, 1) # Passos p/ direita e esquerda
passeio_aleatorio <-
c(0, sample(passos, tamanho_passeio, TRUE) %>% cumsum())
dados_passeio <- data.frame(tempo = 0:tamanho_passeio,
posicoes = passeio_aleatorio)
pacman <- "pacman.png"
dados_passeio %>%
mutate(imagem = pacman) %>%
ggplot(aes(x = tempo,
y = posicoes)) +
theme_minimal() +
geom_path() +
geom_image(aes(image = imagem),
size = 0.1) +
transition_reveal(tempo)
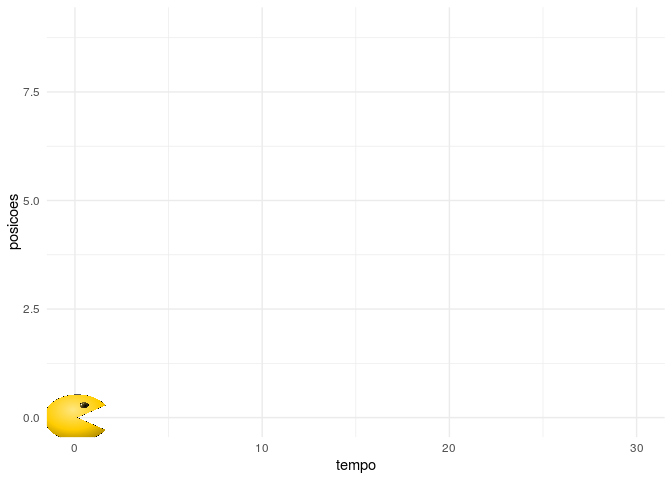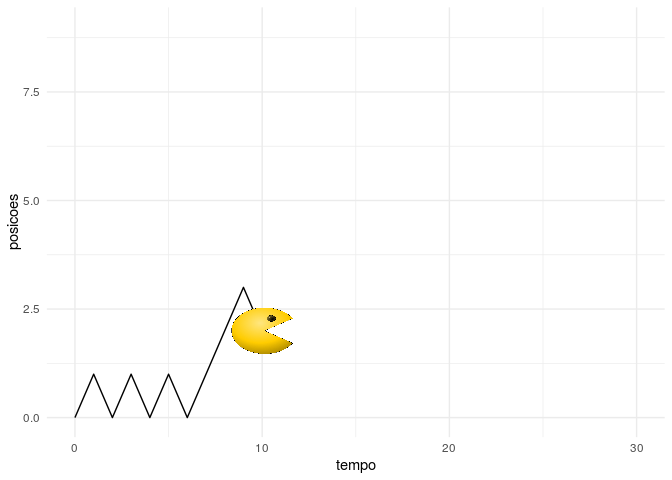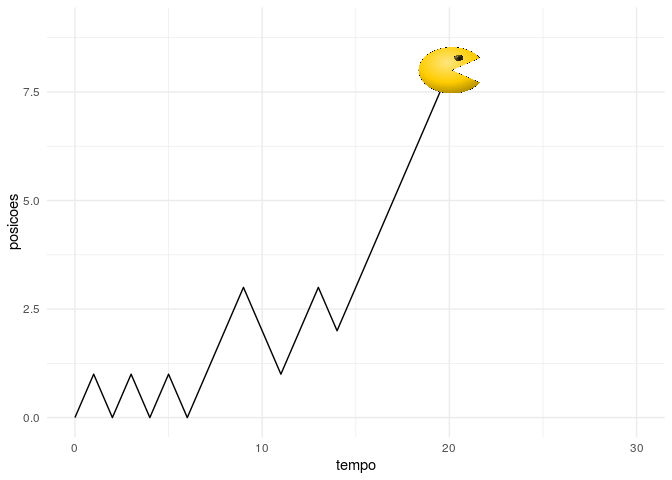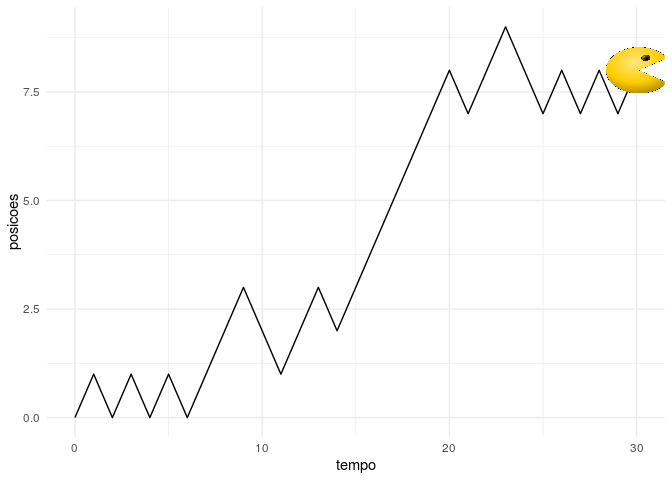
Note que cada vez que rodarmos esse código acima, a trajetória poderá
ser diferente, pois não definimos uma semente com a função set.seed(),
por exemplo. Podemos também considerar diversas trajetórias para
entender algumas das propriedades desse passeio aleatório.
numero_trajetorias <- 6
varios_passeios <- lapply(1:numero_trajetorias, function(x){
passeio_aleatorio <-
c(0, sample(passos, tamanho_passeio, TRUE) %>% cumsum())
dados_passeio <- data.frame(tempo = 0:tamanho_passeio,
posicoes = passeio_aleatorio,
trajetoria = x)
}) %>% do.call(rbind.data.frame, .)
animacao_pacman <-
varios_passeios %>%
mutate(imagem = pacman) %>%
ggplot(aes(x = tempo,
y = posicoes,
group = trajetoria,
colour = factor(trajetoria))) +
theme_minimal() +
theme(legend.position = 'none') +
geom_path() +
geom_image(aes(image = imagem), size = 0.1) +
transition_reveal(along = tempo)
animate(animacao_pacman, renderer = gifski_renderer(),
width = 480, height = 480)
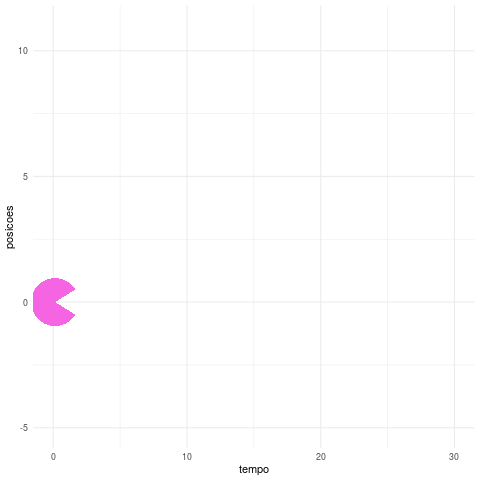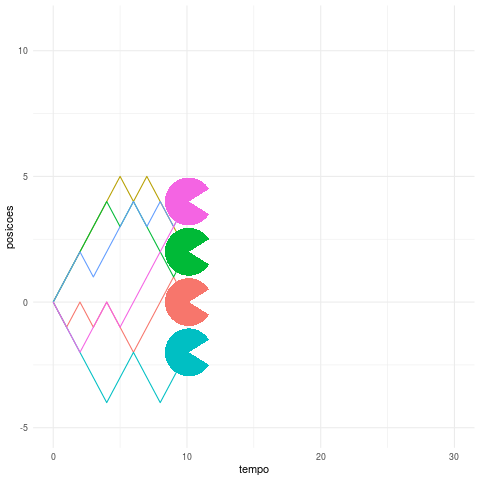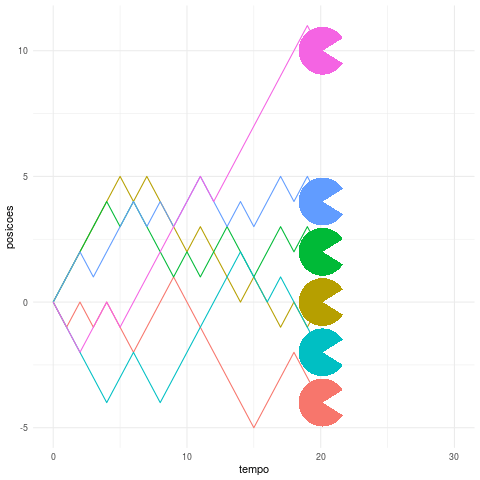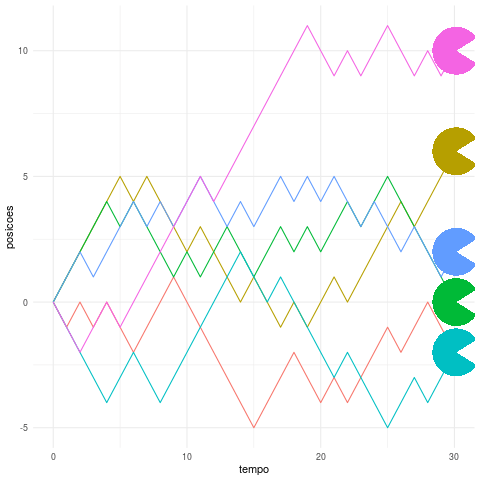
O que essa animação com várias trajetórias nos ajuda a perceber é que, após um certo tempo (t), a variância do local onde o “Pacman” se encontra é proporcional ao tempo (t), ou seja, quanto maior esse valor maior é a incerteza sobre a sua posiçao. Além disso, em média sua posição é sempre igual a sua posição inicial, o que pode parecer um resultado contra-intuitivo tendo em vista a aleatoriedade desse passeio.
Esperamos que tenham gostado dessas animações e em futuros posts podemos retomar essas ferramentas para falar sobre outros resultados estatísticos interessantes.
